Implizites Eulerverfahren
Nachdem ich gerade meinen Osterurlaub verlebe habe ich begonnen, ein Thema anzufassen, das mich schon länger beschäftigt - aber für Mathematik brauch ich Ruhe... Ich wollte zunächst hinter die Magie der impliziten Verfahren steigen und schauen, ob es eien Möglichkeit gibt, diese ebenfalls so generisch zu betrachten, dass man auf einfache Art und Weise ein Framework dafür erstellen kann
Ich stellte dazu zunächst die Verfahren anhand einer einfachen Differentialgleichung ersten Grades gegenüber:
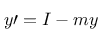Dazu benutzte ich ein kleines Python-Script:
#!/usr/bin/python
'''
Test for implicit and explicit Euler method for
numerically solving differential equations using
y'=i-my as an example and showing instability as
well as slow convergence as disadvantages
in either method
'''
import matplotlib.pyplot as plt
import numpy as np
def f(t):
return 1-np.exp(-t)
t2 = np.arange(0.0, 11.0, 0.02)
h=1.3
m=-1
I=1
x = 0
y= 0
plt.figure(1)
plt.subplot(211)
plt.plot([x],[y],'ro')
while x<10:
ynew=(y+h*I)/(1-m*h)
print " %f " % (ynew)
y=ynew
x=x+h
plt.plot([x],[y],'ro')
plt.plot(t2, f(t2), 'k')
plt.axis([0, 11, 0, 1.5])
h=1.3
m=-1
I=1
x = 0
y= 0
plt.subplot(212)
plt.plot([x],[y],'ro')
while x<10:
ynew=y+h*(I+m*y)
print " %f " % (ynew)
y=ynew
x=x+h
plt.plot([x],[y],'ro')
plt.plot(t2, f(t2), 'k')
plt.axis([0, 11, 0, 1.5])
plt.show()
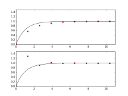
Dieses Skript liefert folgendes Ergebnis (oben das implizite Verfahren, unten das explizite):
Man sieht deutlich die sehr langsame Konvergenz des impliziten Verfahrens - aber auch das Überschwingen und die Instabilität des expliziten Verfahrens bei zu groß gewählter Schrittweite...
Leider ist mir noch keine Möglichkeit eingefallen, wie man das implizite Verfahren so generisch gestalten könnte, dass man einfach die Differentialgleichung in ein Framework fallen lässt und die Berechnung startet: Dafür müsste man sich mit symbolischer Algebra und Reihenentwicklung auseinandersetzen (jedenfalls ist das meine aktuelle Meinung nach Studium des Internet).
Artikel, die hierher verlinken
Visualisierung von Strange Attractors mit Java3D
26.02.2020
Ich wollte mich schon lange mal wieder mit Chaos und Systemen mit Strange Attractors befassen. Schließlich habe ich ja die entsprechende Infrastruktur bereits als Framework für die numerische Behandlung von Differentialgleichungssystemen verfügbar.
Roessler Attractor und implizites Eulerverfahren
26.02.2020
Nachdem ich so viel Spaß bei der Untersuchung der Behandlung eines chaotischen Systems mittels impliziten Eulerverfahrens hatte, habe ich mir gleich noch eines vorgenommen...
Strange Attractors mit BigDecimal
26.02.2020
Nachdem ich mir in meinem früheren Artikel zum Thema der Mathematik mit beliebiger Präzision in Java noch nicht sicher war ob es Sinn machen würde, mein Framework für die numerische Behandlung von Differentialgleichungssystemen auf die Option der Benutzung von BigDecimal als unterliegenden Datentyp zu erweitern, habe ich nun doch damit experimentiert:
Mathematik mit beliebiger Präzision in Java
11.11.2018
Wann immer ich hier über Experimente mit numerischen Lösungsverfahren für Differentialgleichungssysteme berichte, habe ich im Hinterkopf, dass diese Verfahren eigentlich völlig ungeeignet dafür sind, solche Systeme zu analysieren, da heutige Digitalcomputer bereits rationale Zahlen nicht exakt darstellen können - von irrationalen ganz zu schweigen...
Chaotische Systeme und implizites Eulerverfahren
01.10.2018
Nachdem ich erfolgreich einige chaotische Systeme mittels numerischer Verfahren untersucht hatte, reifte in mir der Entschluss, für diese Systeme implizite und explizite numerische Verfahren gegenüberzustellen.
Kommentar hinzufügen (via 
Kommentare ansehen (via 
Vor 5 Jahren hier im Blog
-
Fährnisse des Buildprozesses unter Windows
17.07.2019
Nachdem ich begonnen hatte, mich mit der Beschleunigung der Berechnung des Mandelbrot-Fraktals unter Zuhilfenahme der Shadereinheiten in Graphikkarten zu beschäftigen und erste Erfolge feiern konnte, wollte ich das mal auf einer richtigen Graphikkarte ausprobieren...
Weiterlesen...
Tags
Android Basteln C und C++ Chaos Datenbanken Docker dWb+ ESP Wifi Garten Geo Git(lab|hub) Go GUI Gui Hardware Java Jupyter Komponenten Links Linux Markdown Markup Music Numerik PKI-X.509-CA Python QBrowser Rants Raspi Revisited Security Software-Test sQLshell TeleGrafana Verschiedenes Video Virtualisierung Windows Upcoming...
Neueste Artikel
- Datenvalidierung UTF8 mit BiDi-Steuerzeichen (TrojanSource 2.0)
Ich bin heute nochmal inspiriert worden, weiter über die Trojan Source Vulnerability nachzudenken. Meiner Meinung nach bestehen hier noch Probleme - speziell bei Nutzereingaben oder Daten, die über externe Schnittstellen ampfangen werden.
Weiterlesen... - OpenStreetMap Navi als Docker-Container
Ich habe die auf OpenStreetMap basierende OpenSource Navigationslösung Graphhopper in einen Docker-Container gepackt und als neuestes Mitglied in meinem Docker-Zoo willkommen geheißen.
Weiterlesen... - SQL-Aggregatfunktionen in SQLite als BeanShell-Scripts
Ich habe neulich über eine Möglichkeit berichtet, SQLite mittels der sQLshell und Beanshell-Skripten um SQL-Funktionen zu erweitern. In diesem Artikel versprach ich auch, über eine solche Möglichkeit für Aggregatfunktionen zu berichten.
Weiterlesen...
Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.
Wer daran teilhaben und eventuell sogar davon profitieren möchte, muß damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.
Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...
PS: Meine öffentlichen GitHub-Repositories findet man hier - meine öffentlichen GitLab-Repositories finden sich dagegen hier.