Updates

• 26. Februar 2020

Ich wollte nach längerer Zeit wieder einmal in die Welt chaoticher Systeme eintauchen und habe mich dazu mit zwei Systemen beschäftigt...

Das Van-der-Pol-System ist ein relativ einfaches zweidimensionales System, das aus einer einzelnen Differentialgleichung zweiter Ordnung besteht. 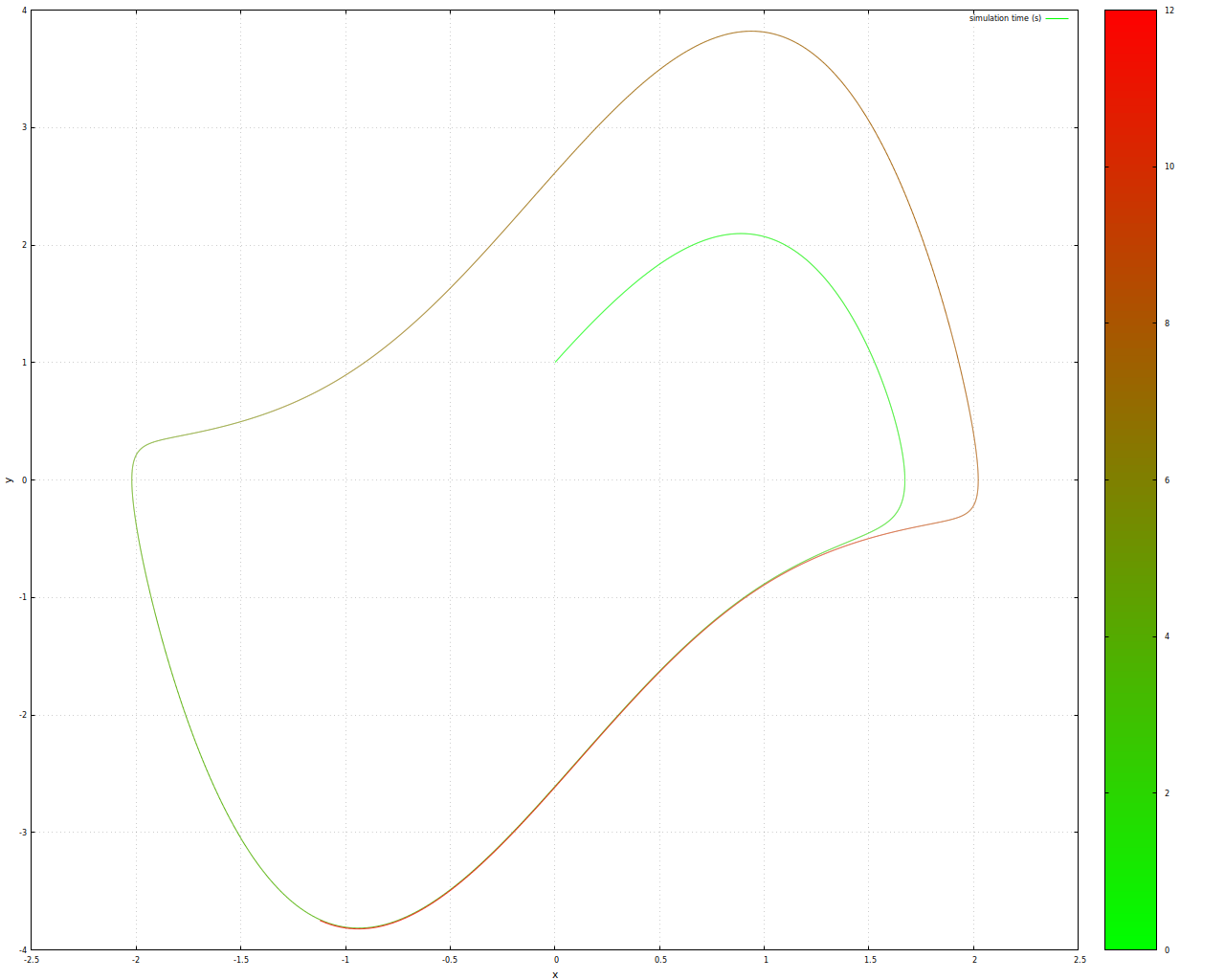Phasendiagramm Van-derPol-System

In dieser Abbildung kann man noch nicht so richtig erkennen, warum es dieses System auf die Liste der chaotischen geschafft hat - extrem hineingezoomt kann man aber ein ergodisches Verhalten zumindest erahnen:

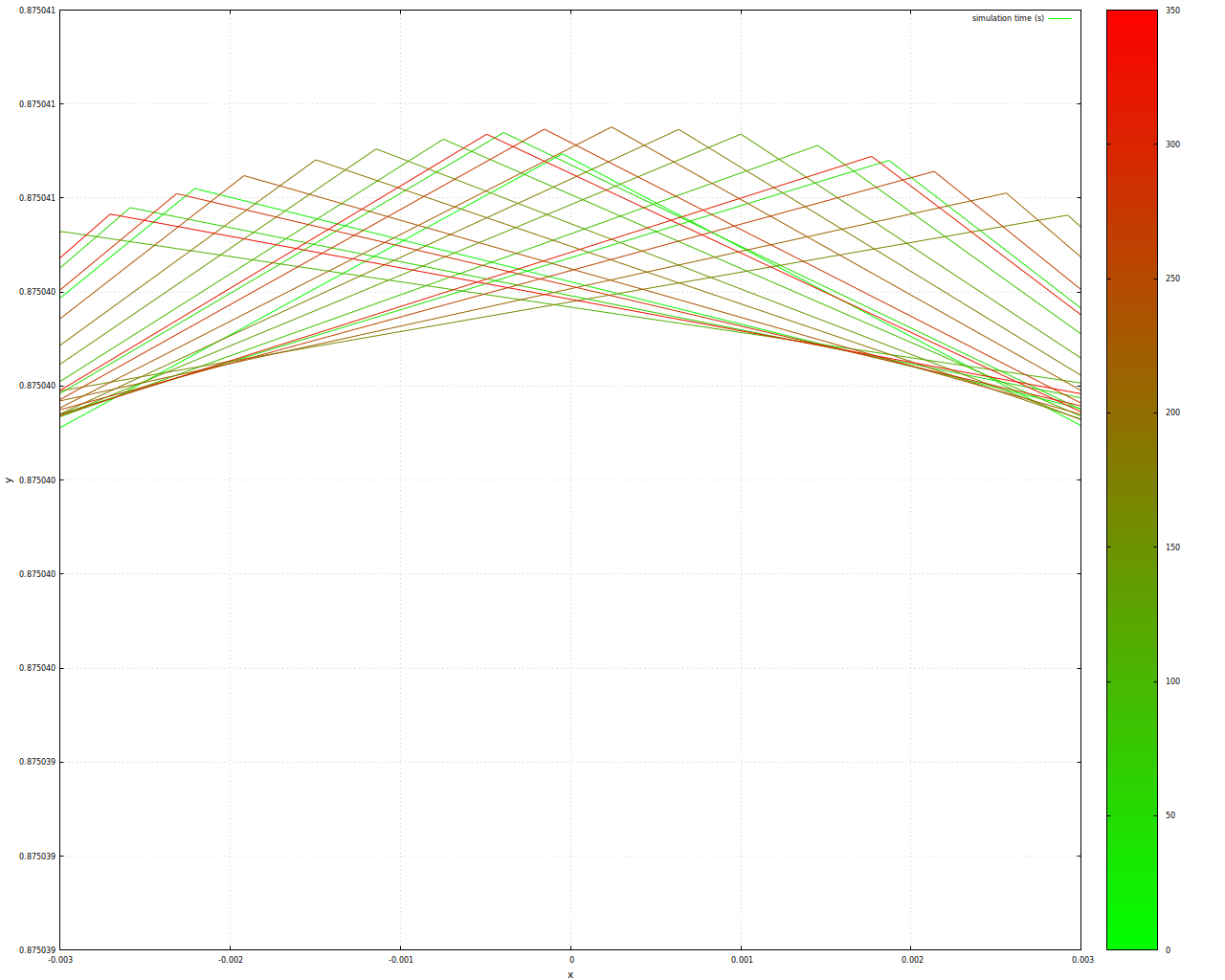Phasendiagramm Van-derPol-System - stark vergrößerter Ausschnitt

Hier könnte man natürlich bereits wieder zweifeln, ob dieses Verhalten nicht ein Artefakt des benutzten numerischen Verfahrens darstellt...

Das zweite System, mit dem ich mich beschäftigt habe ist eigentlich kein System, sondern eine Klasse von solchen.

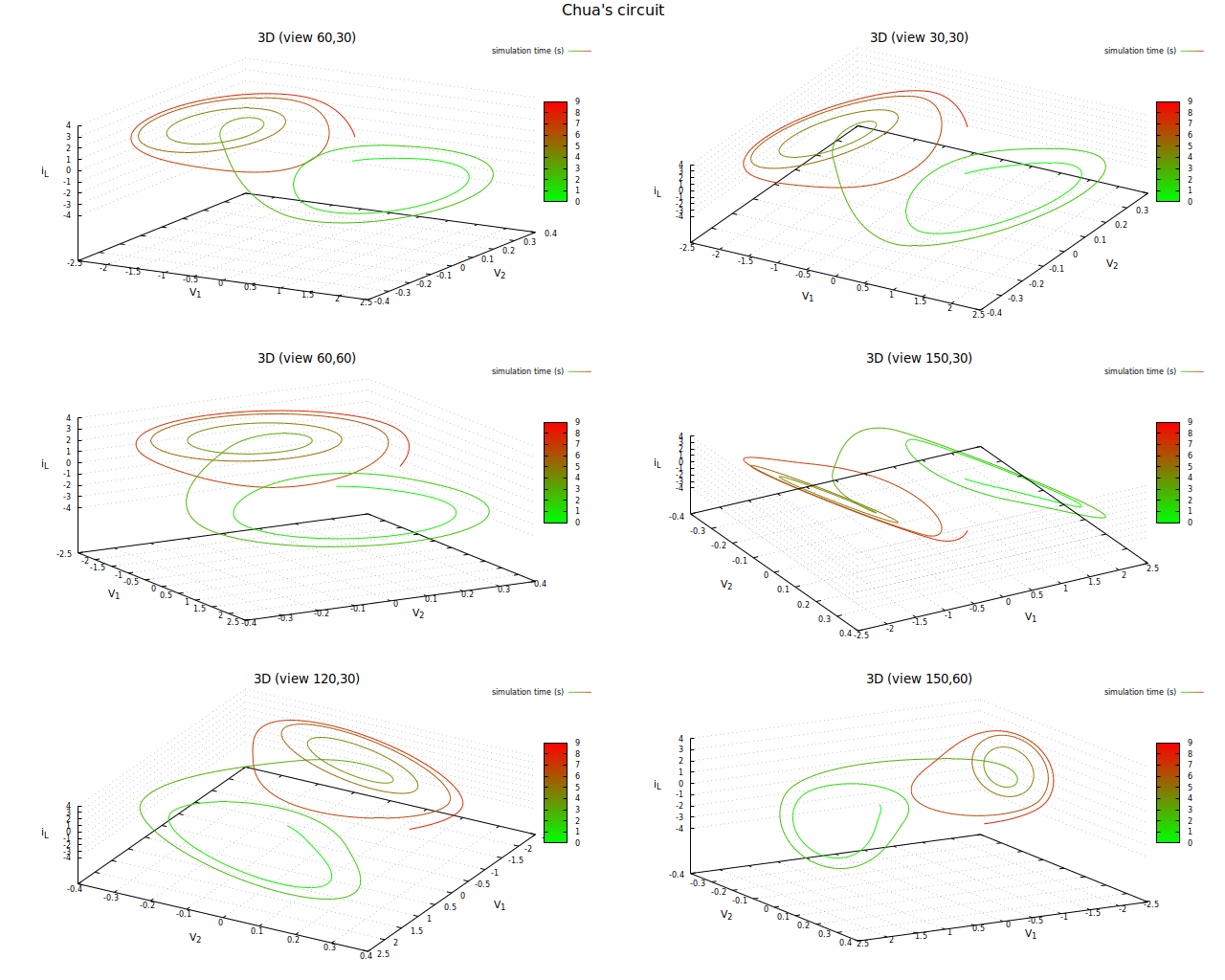Dreidimensionale Darstellung des Phasenraums eines Chua-Systems

Wunderbarerweise sehen wir hier einen Double-Scroll-Attraktor, wie ihn zum Beispiel auch das Lorenz-System aufweist.

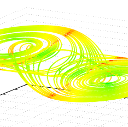
Interessant ist dieses System auch aus einem anderen Grund: In der vorhergehenden Graphik war die Darstellung eigentlich vierdimensional: die Farbe zeigte den zeitlichen Verlauf der Berechnung an. Benutzt man statt dessen als vierte Dimension die Schrittweite des für die Berechnung benutzten numerischen Verfahrens zur Lösung von Differentialgleichungen (ich habe eines mit adaptiver Schrittweitensteuerung benutzt), so erkennt man Hotspots - Bereiche, in denen die Schrittweite besonders klein gewählt wurde (rot dargestellt). Lässt man das System für eine längere Zeitspanne berechnen und wählt man die Strichstärke der Visualisierung ein klein wenig größer, ergeben sich fast schon Flächen, auf denen diese Hotspots an gerade Linien oder Streifen erinnern:

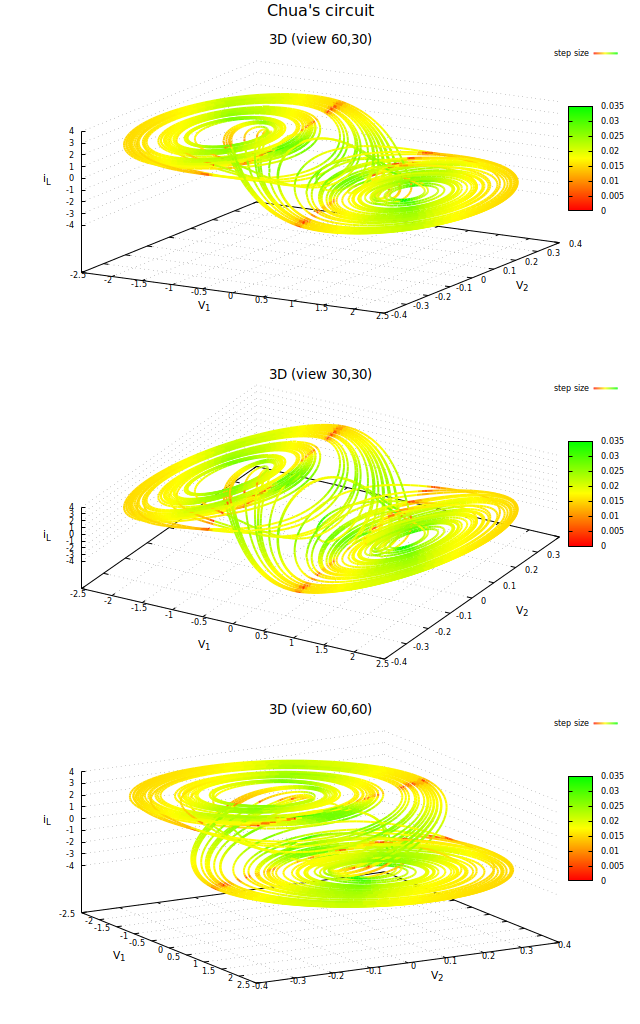Dreidimensionale Darstellung des Phasenraums eines Chua-Systems mit farbig kodierter Schrittweite des numerischen Verfahrens

Dies kann man sich auch intuitiv hervorragend erklären: Dort knicken die beiden Scheiben in die Übergangsphase ab - dort ist also auch zu erwarten, dass die Krümmung der Trajektorien besonders groß wird. Da numerische Verfahren den Verlauf der exakten Lösung immer durch stückweise lineare Segmente approximieren würde dort der Fehler einer solchen Approximation daher besonders groß. Verfahren mit adaptiver Schrittweitensteuerung schätzen den Fehler und passen damit die Schrittweite an - daher ist in Gebieten relativ großer Krümmung eine relativ kleine Schrittweite zu erwarten!

Aktualisierung vom 26. Februar 2020

Artikel, die hierher verlinken

Kommentar hinzufügen (via ) Kommentare ansehen (via )

Kommentar hinzufügen (via ) Kommentare ansehen (via )