Updates
Nachdem ich nun schon längere Zeit nichts mehr über Chaos und nichtlineare Systeme geschrieben habe, habe ich meinen Urlaub dazu genutzt, mich des Fermi-Pasta-Ulam–Tsingou-Experiments anzunehmen. Hier meine Ergebnisse...
Dieses Experiment gilt als eines der ersten Computerexperimente. Es erwies sich, dass das erwartete Verhalten vom simulierten Ergebnis deutlich abwich: Das Experiment simulierte n nichtlinear gekoppelte Schwinger. Die Erwartung war, dass das System in endlicher Zeit thermalisiert - das bedeutet, dass alle Schwingungsmoden gleich angeregt werden und die bestimmende Frequenz sich abschwächen sollte.
Was allerdings beobachtet wurde war, dass nach einer bestimmten Zeit ein quasi-periodisches Verhalten in der Simulation beobachtbar war. Diese Beobachtung wurde zunächst auf Fehler in der Berechnung zurückgeführt. Nachdem dies ausgeschlossen war, wurden verschiedene Lösungsansätze überprüft. Das Experiment trieb das damals noch recht neue Feld der Erforschung nichtlinearer Systeme stark an (Stichwort Chaos, Ergodizität), gilt heute jedoch weitestgehend als verstanden.
Das ursprüngliche Experiment stellte ein eindimensionales Experiment dar, im zwei- und dreidimensionalen Fall beginnt die Untersuchung solcher Systeme gerade - unter anderem wegen der enormen Herausforderungen bei der numerischen Behandlung.
Meine Versuche, das Experiment nachzustellen unternahm ich mit n=32 gekoppelten Nodes und quadratischer Nichtlinearität:
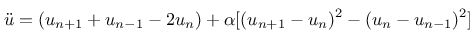
Ich habe hier zunächst den zeitlichen Verlauf des Zustandes von 5 ausgewählten Nodes über den gesamten Verlauf der Simulation dargestellt. Die initiale Anregung des Systems war eine Hälfte einer Sinusschwingung: die Nodes links und rechts hatten initial den Zustand 0.0 angenommen, Node 15 und 16 simultan den Zustand 1.0.
 Verlauf der Zustände über das gesamte Experiment hinweg.
Verlauf der Zustände über das gesamte Experiment hinweg.
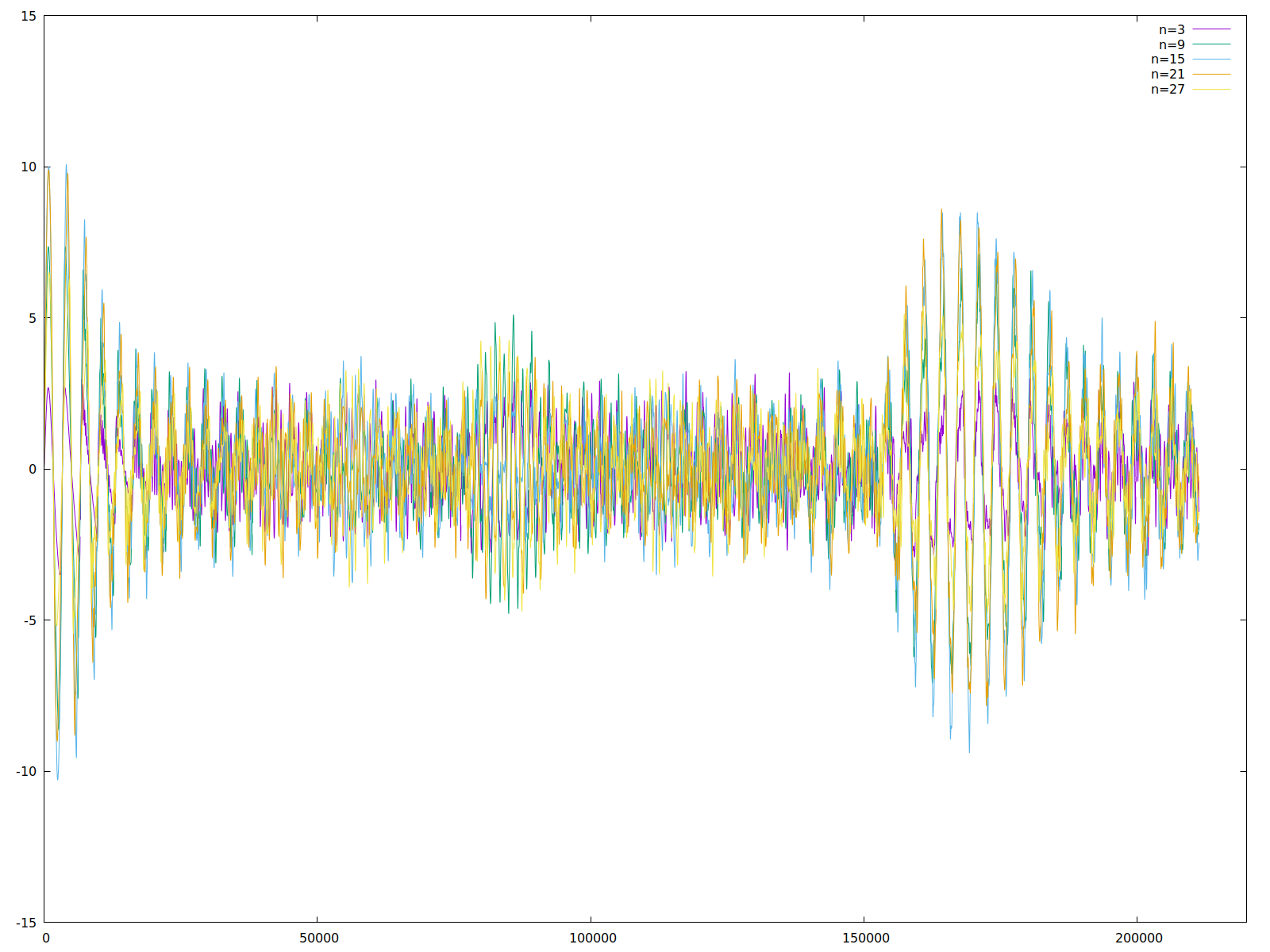
Man sieht hier deutlich, dass anfangs alle Nodes phasengleich zu schwingen scheinen - damit ist die initiale Mode immer noch aktiv.
 Zoom auf die ersten 10000 Zeitschritte - Man erkennt deutlich die synchrone Phasenlage aller Nodes.
Zoom auf die ersten 10000 Zeitschritte - Man erkennt deutlich die synchrone Phasenlage aller Nodes.
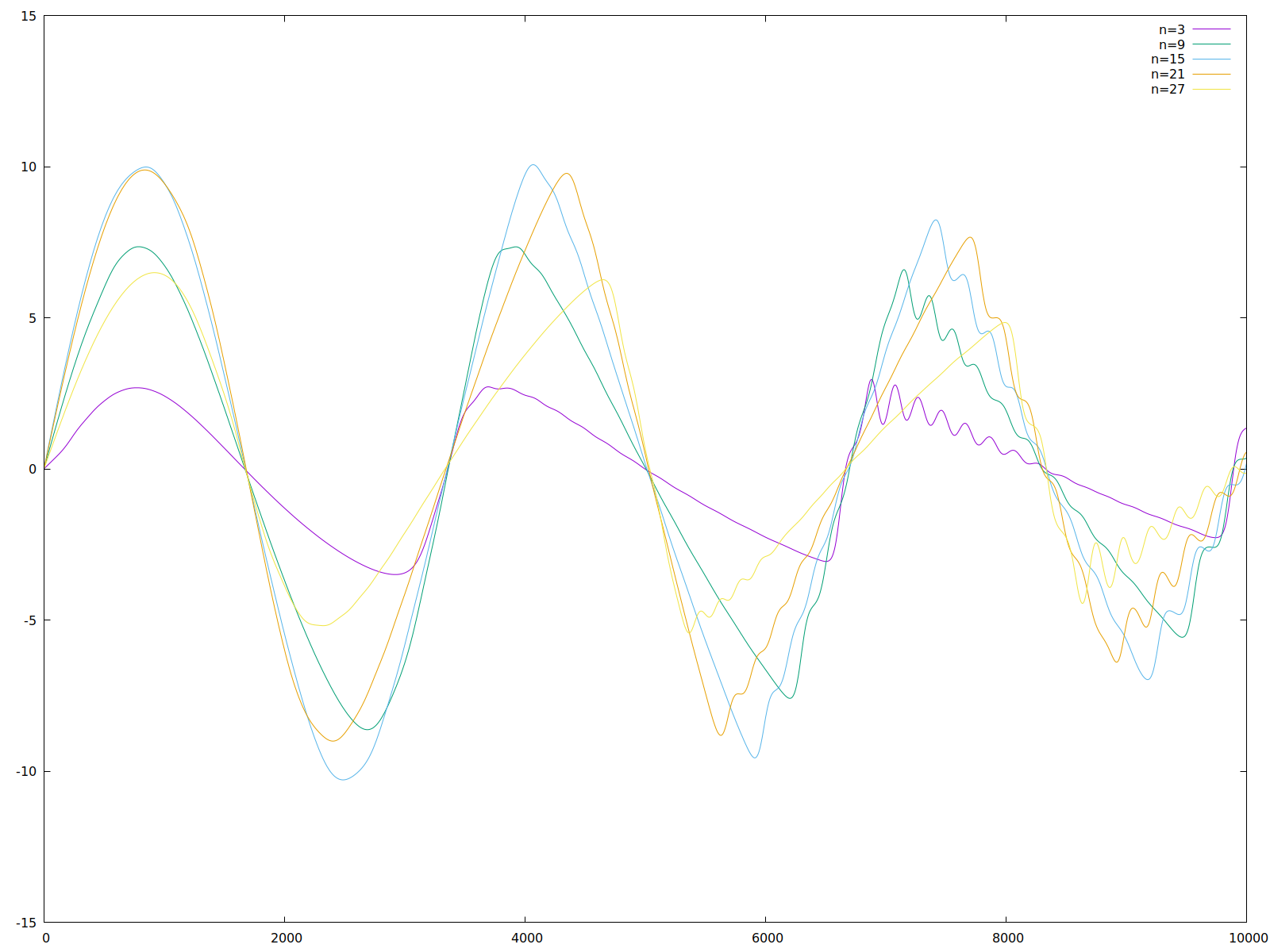
Allerdings schwächt sich diese Synchronität bereits ab Schritt 15000 deutlich ab - ein Zoom auf den Bereich zwischen 50000 und 60000 Schritten verdeutlicht dies nochmals:
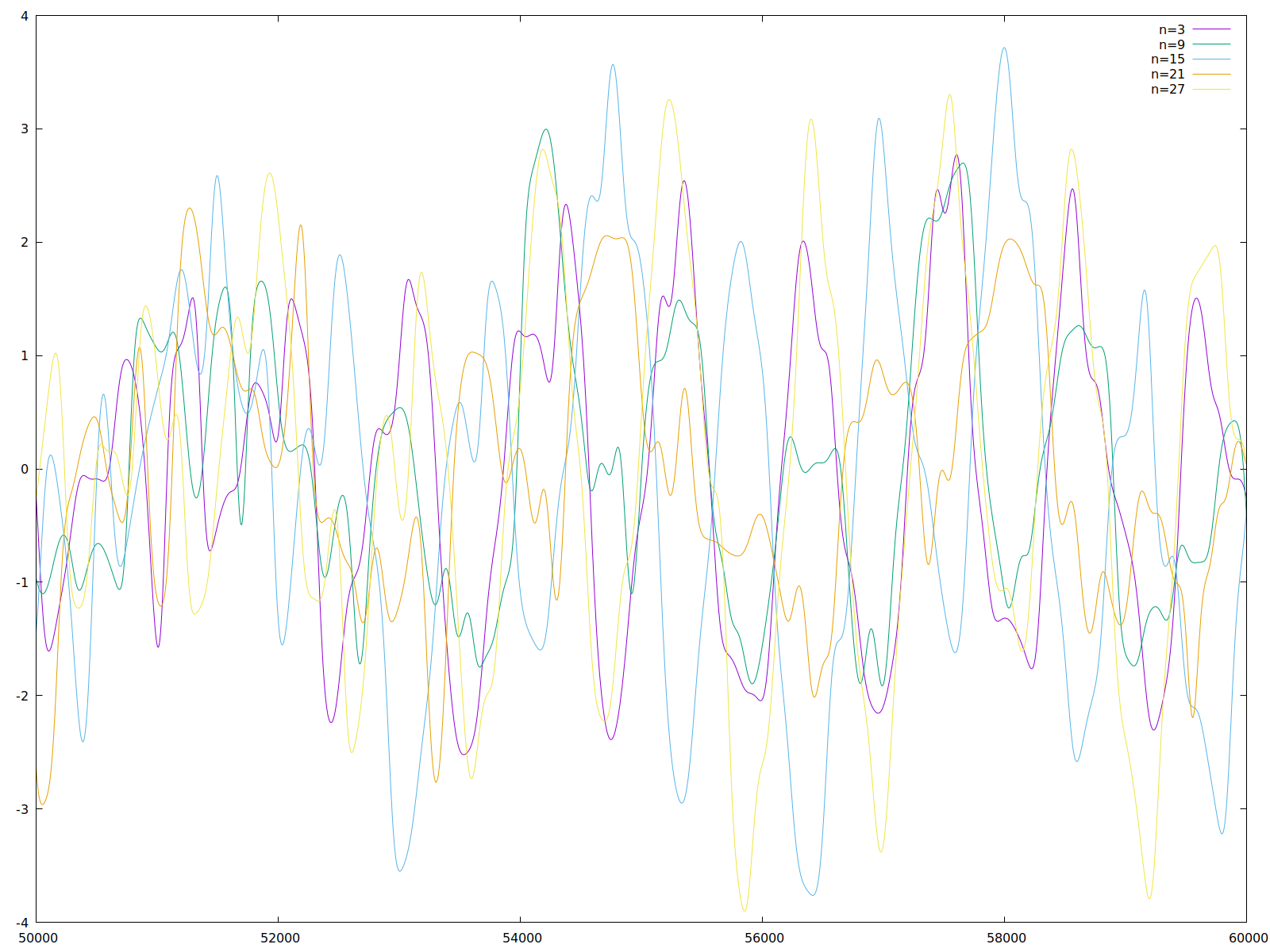 Zoom auf den Bereich zwischen 50000 und 6000 Schritten.
Zoom auf den Bereich zwischen 50000 und 6000 Schritten.
In der Darstellung des gesamten Experiments war allerdings auch weiter rechts ein Abschnitt zu sehen, der stark an die ersten 10000 Schritte erinnert hat - daher hier ein Zoom in diesen Bereich:
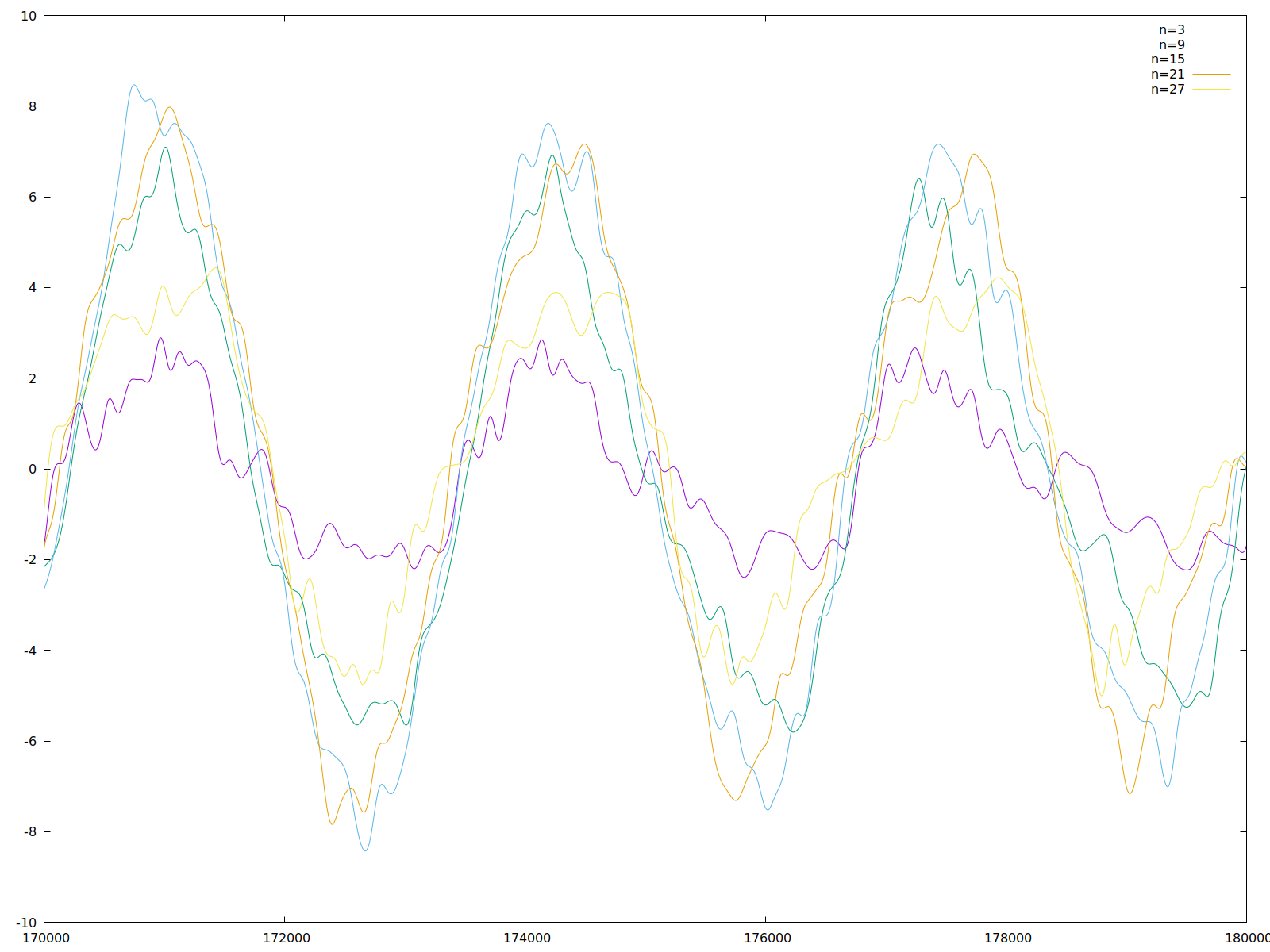 Zoom auf den Bereich zwischen 170000 und 180000 Schritten.
Zoom auf den Bereich zwischen 170000 und 180000 Schritten.
Man sieht, dass nicht nur die Phasenlage wieder fast identisch ist, sondern dass auch die Verläufe der Zustände einzelner Nodes fast vollkommen frei von Oberwellen sind.
Der Vollständigkeit halber möchte ich hier noch eine Darstellung der Zustände derselben Nodes im Falle des Fehlens der Nichtlinearität nachreichen - Man erkennt: von Chaos keine Spur, die Phasenlage der Nodes zueinander bleibt über das gesamte Experiment hin exakt synchron.
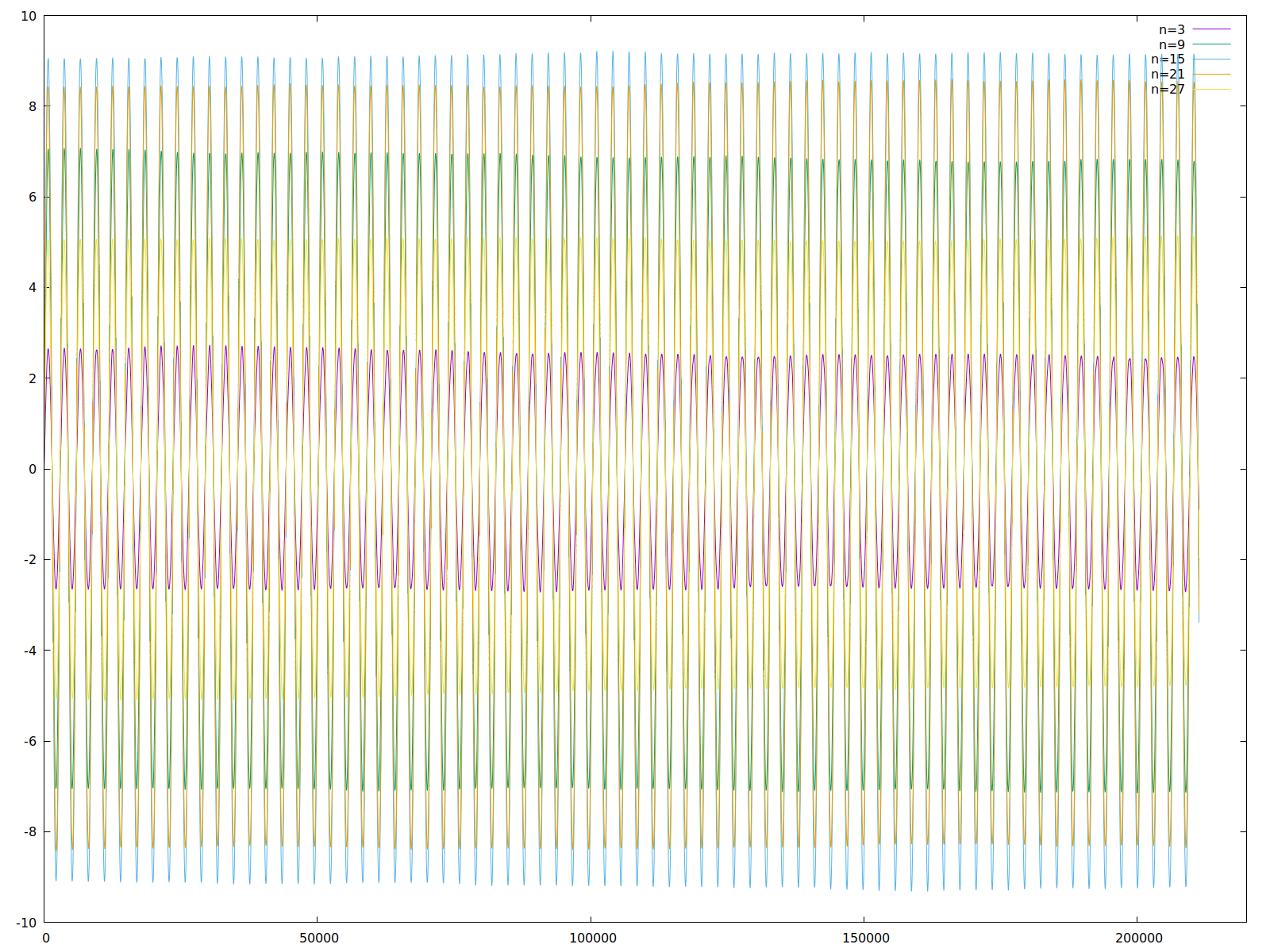 Verlauf der Zustände bei fehlender Nichtlinearität über das gesamte Experiment hinweg.
Verlauf der Zustände bei fehlender Nichtlinearität über das gesamte Experiment hinweg.
Diese Ergebnisse lassen sich mittels eines Videos nochmal besser veranschaulichen: Das Video stellt den zeitlichen Verlauf der Zustände aller Nodes dar. Dabei gleitet ein Fenster der Breite 1000 Schritte über die Darstellung. Man erkennt deutlich die niederfrequente Anregung zu Beginn des Experiments, die aber bereits nach ungefähr 5000 Schritten von deutlichen Oberwellen überlagert wird. Nach 8000 Schritten werden diese dann so stark, dass die ursprüngliche Anregung fast vollständig überdeckt ist. Nach 60000 Schritten ist von der ursprünglichen Anregung nichts mehr zurückgeblieben - das Chaos regiert. Nach 165000 Schritten kehrt die ursprüngliche Anregung dann plötzlich wieder - fast gänzlich oberwellenfrei.
Aktualisierung vom 21. April 2019
Vor 5 Jahren hier im Blog
-
Fährnisse des Buildprozesses unter Windows
17.07.2019
Nachdem ich begonnen hatte, mich mit der Beschleunigung der Berechnung des Mandelbrot-Fraktals unter Zuhilfenahme der Shadereinheiten in Graphikkarten zu beschäftigen und erste Erfolge feiern konnte, wollte ich das mal auf einer richtigen Graphikkarte ausprobieren...
Weiterlesen...
Tags
Android Basteln C und C++ Chaos Datenbanken Docker dWb+ ESP Wifi Garten Geo Git(lab|hub) Go GUI Gui Hardware Java Jupyter Komponenten Links Linux Markdown Markup Music Numerik PKI-X.509-CA Python QBrowser Rants Raspi Revisited Security Software-Test sQLshell TeleGrafana Verschiedenes Video Virtualisierung Windows Upcoming...
Neueste Artikel
- Datenvalidierung UTF8 mit BiDi-Steuerzeichen (TrojanSource 2.0)
Ich bin heute nochmal inspiriert worden, weiter über die Trojan Source Vulnerability nachzudenken. Meiner Meinung nach bestehen hier noch Probleme - speziell bei Nutzereingaben oder Daten, die über externe Schnittstellen ampfangen werden.
Weiterlesen... - OpenStreetMap Navi als Docker-Container
Ich habe die auf OpenStreetMap basierende OpenSource Navigationslösung Graphhopper in einen Docker-Container gepackt und als neuestes Mitglied in meinem Docker-Zoo willkommen geheißen.
Weiterlesen... - SQL-Aggregatfunktionen in SQLite als BeanShell-Scripts
Ich habe neulich über eine Möglichkeit berichtet, SQLite mittels der sQLshell und Beanshell-Skripten um SQL-Funktionen zu erweitern. In diesem Artikel versprach ich auch, über eine solche Möglichkeit für Aggregatfunktionen zu berichten.
Weiterlesen...
Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.
Wer daran teilhaben und eventuell sogar davon profitieren möchte, muß damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.
Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...
PS: Meine öffentlichen GitHub-Repositories findet man hier - meine öffentlichen GitLab-Repositories finden sich dagegen hier.

 )
)




