Inspiriert durch einen Fund im Internet habe ich versucht, meinen Landschaftsgenerator um einen weiteren Renderer zu ergänzen.

Ich habe bisher die Ergebnisse meines Landschaftsgenerators auf verschiedene Weisen visualisiert - da gab es die selbstgeschriebene 3D-Visualisierung, die Java3d-Variante und auch eine Voxel-Variante wurde bereits in freier Wildbahn beobachtet.

Durch diesen Link, auf den ich über Mastodon gestoßen bin wurde ich inspiriert, mich an einem isometrischen Renderer zu versuchen.

Dabei galt es, zwei Probleme zu lösen - das eine war der Algorithmus und das andere die benötigten graphischen Ressourcen zu beschaffen.

Problem zwei war mittels des Internets schnell gelöst - die noch fehlenden von mir benötigten Varianten wurden aus den verfügbaren mittels Gimp erzeugt (für meine Zwecke benötigte ich noch Darstellungen von Wasser und Felsen).

Der Algorithmus schließlich wurde von mir tatsächlich selbst geschrieben - ich wollte eigentlich die bereits hier geleistete Vorarbeit benutzen, aber diese Sprache war so weit außerhalb meiner Komfortzone, dass ich es am Ende doch selber in Java implementierte.

Dabei stellten sich mir folgende Herausforderungen: ein rechteckiges Höhenfeld muss von einer Ecke aus beginnend diagonal durchlaufen werden. Dies erreichte ich, indem ich mich an meine fast 30 Jahre zurückliegenden Mathe-Vorlesungen und speziell den Beweis erinnerte, dass die Menge der rationalen Zahlen abzählbar unendlich ist.

Daraus entstand ein java.util.Iterator, der für eine zweidimensionale Matrix, die in x und y Richtung potentiell unendlich ist alle Tupel geordnet durchläuft.

Darauf aufbauend erstellte ich eine Koordinatentransformation, die zu jedem Punkt (x,y) ein Tupel (d,r) berechnet, das die Nummer der Diagonalen und den Abstand des jeweiligen Punktes von dieser Diagonalen bestimmt. Dabei gilt:

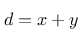
Das Ergebnis ist für einen kleinen Ausschnitt der Ebene hier dargestellt:

 000 001 002 003 004 005 006 007 008 009 010 011 012
 001 002 003 004 005 006 007 008 009 010 011 012 013
 002 003 004 005 006 007 008 009 010 011 012 013 014
 003 004 005 006 007 008 009 010 011 012 013 014 015
 004 005 006 007 008 009 010 011 012 013 014 015 016
 005 006 007 008 009 010 011 012 013 014 015 016 017
 006 007 008 009 010 011 012 013 014 015 016 017 018
 007 008 009 010 011 012 013 014 015 016 017 018 019
 008 009 010 011 012 013 014 015 016 017 018 019 020
 009 010 011 012 013 014 015 016 017 018 019 020 021

Ebenso gilt:

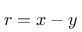
Auch hier das Ergebnis für einen kleinen Ausschnitt der Ebene:

 000 001 002 003 004 005 006 007 008 009 010 011 012
 -01 000 001 002 003 004 005 006 007 008 009 010 011
 -02 -01 000 001 002 003 004 005 006 007 008 009 010
 -03 -02 -01 000 001 002 003 004 005 006 007 008 009
 -04 -03 -02 -01 000 001 002 003 004 005 006 007 008
 -05 -04 -03 -02 -01 000 001 002 003 004 005 006 007
 -06 -05 -04 -03 -02 -01 000 001 002 003 004 005 006
 -07 -06 -05 -04 -03 -02 -01 000 001 002 003 004 005
 -08 -07 -06 -05 -04 -03 -02 -01 000 001 002 003 004
 -09 -08 -07 -06 -05 -04 -03 -02 -01 000 001 002 003

Daraus lassen sich - bei bekannten Dimensionen der zum Rendering verwendeten Kacheln oder Tiles - die exakten Pixelkoordinaten jeder einzelnen Kachel berechnen. Zum Abschluss eine Demonstration des erreichten Ergebnisses:

Isometrisches Rendering eines künstlichen Beispiels

Dieses Ergebnis war nur eine Zwischenstation auf dem Weg zum eigentlichen Ziel: die Ergebnisse des Landschaftsgenerators mittels isometrischer Darstellung zu visualisieren: Der Renderer wurde nochmals überarbeitet in Bezug auf Performance und die Möglichkeit, ein und dasselbe zugrundeliegende Modell wahlweise aus vier verschiedenen Richtungen darzustellen: mit Blick nach Nord, Süd, Ost und West. Die Ergebnisse dessen sind in den folgenden vier Abbildungen eines generierten Landschaftsmodells mit 256x256 Stützstellen zu sehen. Die Höhenwerte sind dazu in 18 Höhenstufen diskretisiert worden:

Isometrisches Rendering einer generierten Landschaft mit Blickrichtung nach Norden

Isometrisches Rendering einer generierten Landschaft mit Blickrichtung nach Osten

Isometrisches Rendering einer generierten Landschaft mit Blickrichtung nach Süden

Isometrisches Rendering einer generierten Landschaft mit Blickrichtung nach Westen

Kommentar hinzufügen (via ) Kommentare ansehen (via )

Kommentar hinzufügen (via ) Kommentare ansehen (via )