Updates

• 15. März 2022

Ich habe bereits vor einiger Zeit über Methoden zur Erzeugung von Karten - etwa Stadtplänen oder Labyrinthen zum Beispiel für Computerspiele berichtet.

Ich habe mich aber bei beiden verlinkten Ergebnissen an der Regularität, die immer noch darin enthalten war gestört: Die Grundlage für diese Ergebnisse war immer ein Gitter von miteinander verbundenen Rechtecken. Ich wollte von dieser Beschränkung loskommen und dachte an Voronoi-Polygone als Grundlage für solche Generatoren statt der üblichen Rechtecke.

Man benötigt aber die explizite parametrische Form der Polygone - oder anders gesagt: die Eckpunktkoordinaten, um sie als Grundlage eines Graphen zur weiteren Bearbeitung nutzen zu können. Es stellte sich bei meinen Recherchen heraus, dass genau diese Form aber nicht einfach erhältlich ist. Ich fand zwar einige Algorithmen, die Voronoi-Polygone erzeugen, die dann aber genau die Koordinaten der Eckpunkte nicht als Ergebnis haben, sondern den zugrundeliegenden Vektorraum einfach nur partitionieren.

Da ich (vorerst) nur an zweidimensionalen Vektorräumen Interesse hatte dachte ich mir, dass es doch möglich sein müsste, einen eigenen Algorithmus zu implementieren. Dabei fing ich natürlich nicht von vorne völlig neu an sondern stützte mich auf vorhandene Algorithmen.

Ich möchte das Vorgehen an einigen Illustrationen dokumentieren - Gehen wir zunächst von einigen zufällig generierten zweidimensionalen Punkten aus, die die Zentren der zu erzeugenden Voronoi-Polygone darstellen sollen:

Zufällig erzeugte Punkte

Für diese Punkte wird anschließend mittels des Bowyer-Watson-Algorithmus die Delauney Triangulation berechnet - das Ergebnis ist ein Netzwerk von Dreiecken wie hier dargestellt:

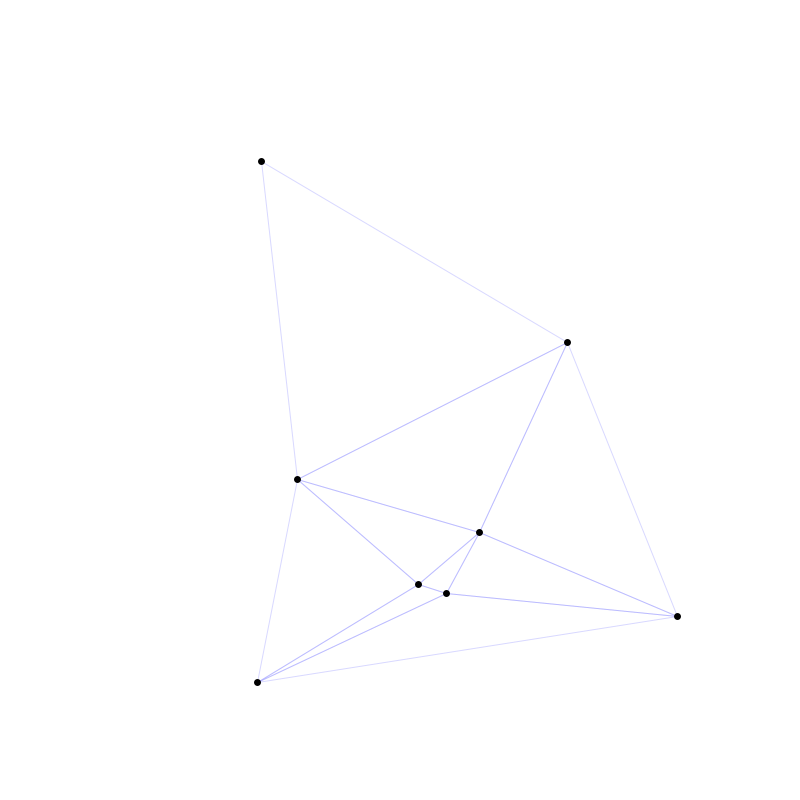Ergebnis der Delauney Triangulation

Für jedes der im Netzwerk enthaltenen Dreiecke wird anschließend der Umkreis bestimmt:

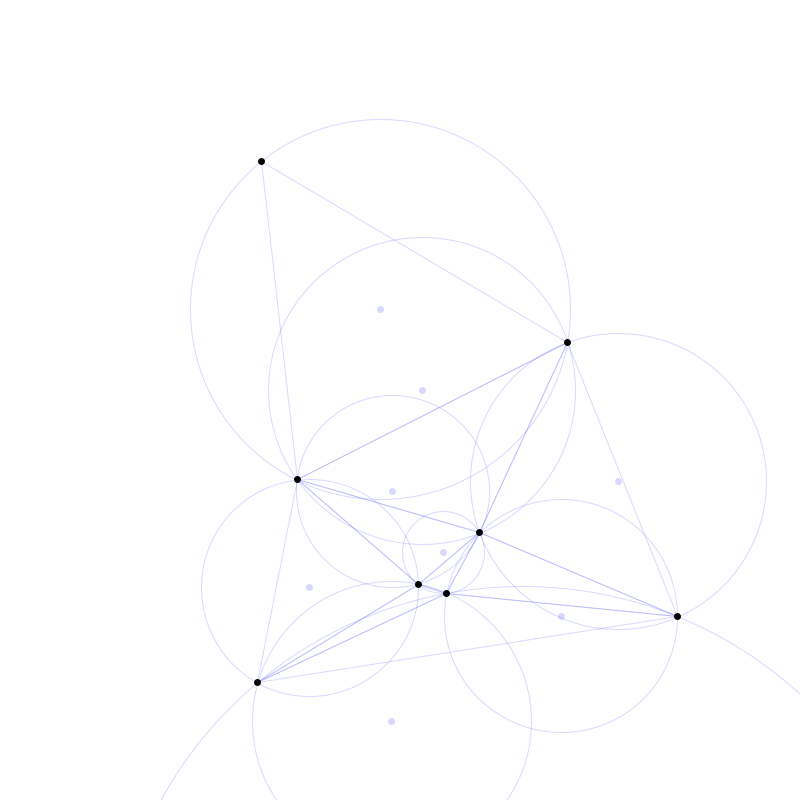Umkreise der durch die Delauney Triangulation gewonnenen Dreiecke

Die Mittelpunkte dieser Umkreise können miteinander verbunden werden - Dadurch ergeben sich Liniensegmente, die genau den Begrenzungen der gesuchten Voronoi-Polygone entsprechen:

Seiten der Vornoi-Polygone

Man sieht aber leicht, dass durch dieses Verfahren nicht alle benötigten Begrenzungen der Voronoi-Polygone gefunden werden können. Daher habe ich folgende Ergänzungen zum Algorithmus hinzugefügt: Zunächst werden die Außenkanten des als Graph aufgefassten Delauney Triangulationsergebnisses gesucht:

Außenkanten des Graphen aus der Delauney Triangulation

Anschließend werden darauf die Mittelsenkrechten konstruiert:

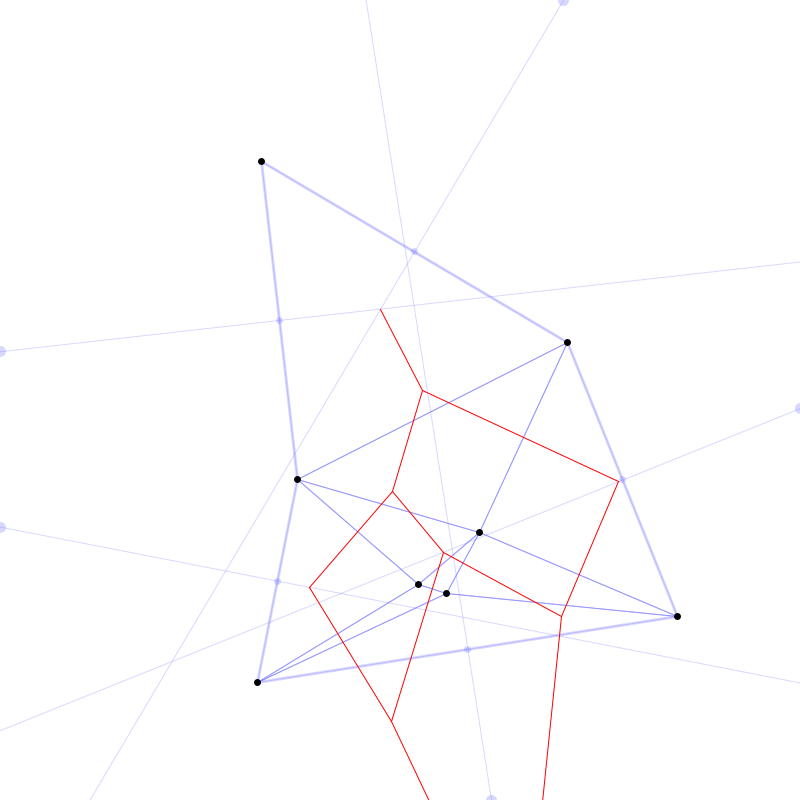Mittelsenkrechte auf den Außenkanten

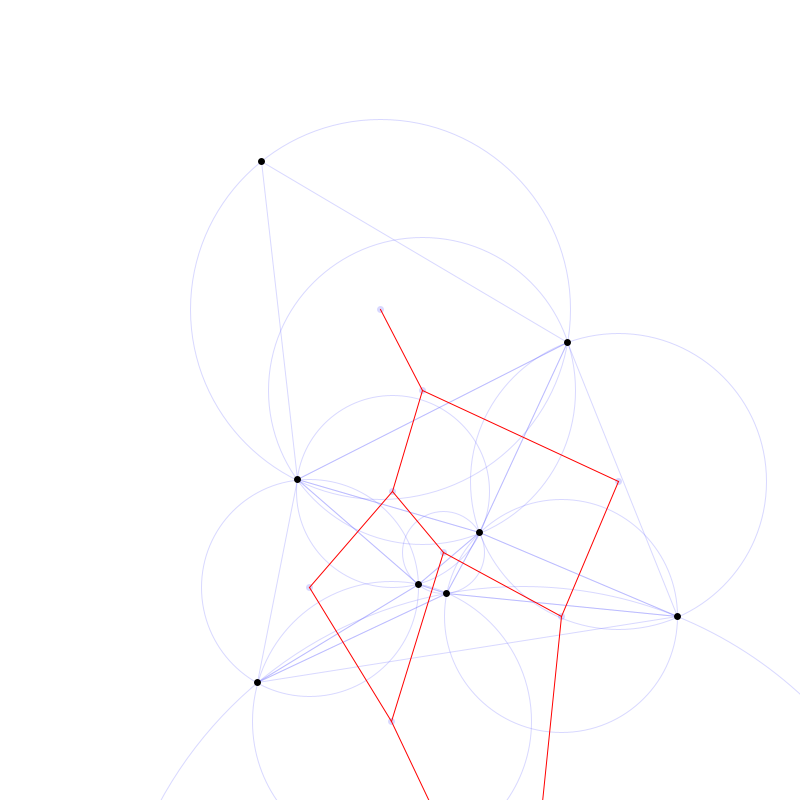
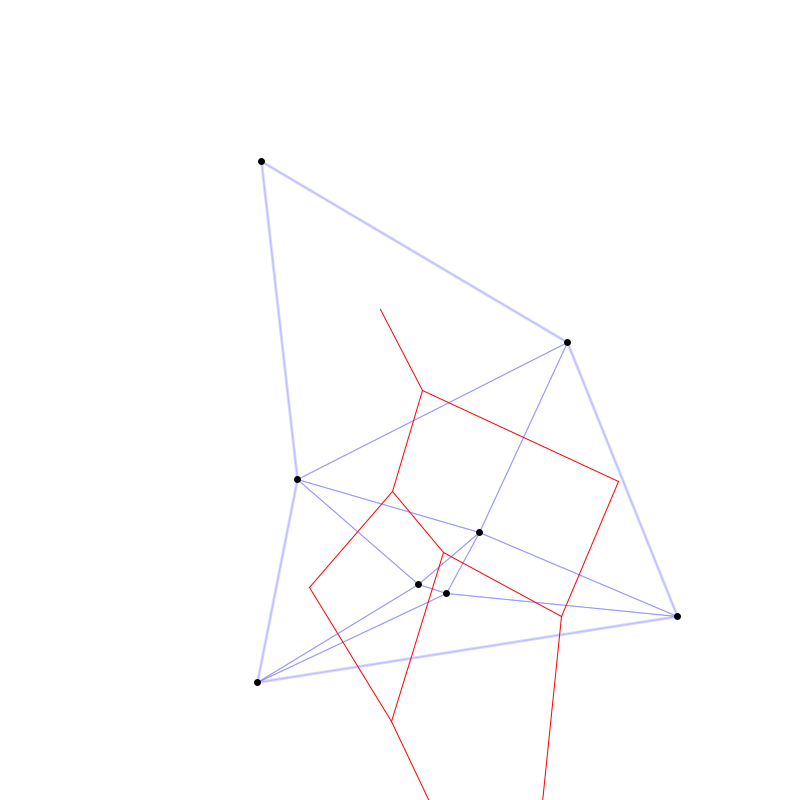
Anschließend wird der kürzere Abschnitt jeder Mittelsenkrechten (gemessen bis zum Rand) in die Menge der Begrenzungen der Voronoi-Polygone aufgenommen. Schließlich werden aus den Schnittpunkten dieser Mittelsenkrechten mit dem Rand weitere zusätzliche Begrenzungen für Voronoi-Polygone am Rand entlang aufgenommen - im nachfolgenden Bild sind diese dick und rot markiert:

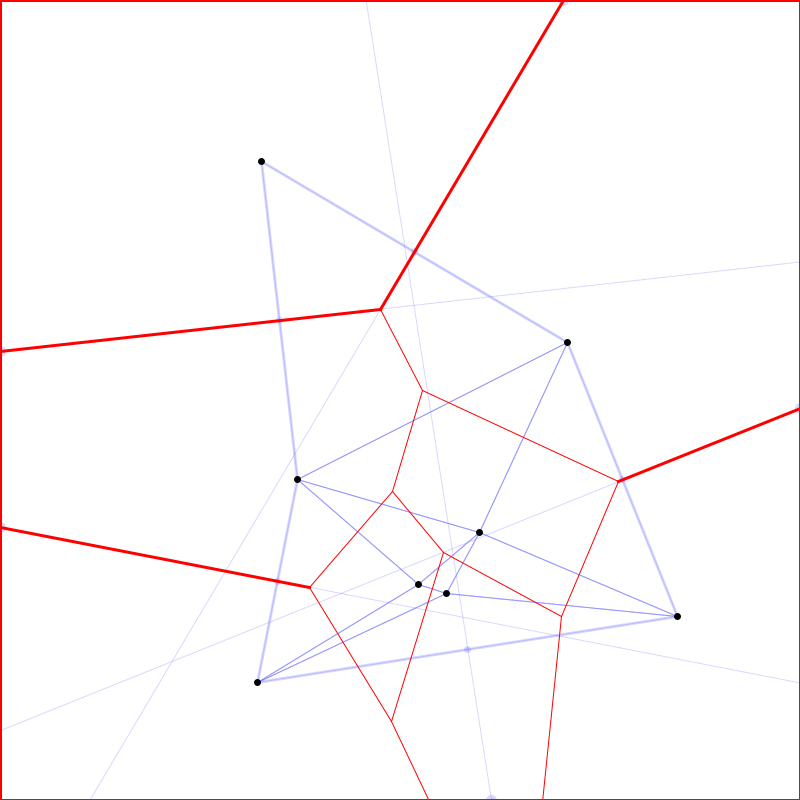Himzufügen fehlender Begrenzungen für Voronoi-Polygone

Damit hat man eine geschlossene Darstellung aller Kanten aller enthaltenen Voronoi-Polygone und kann die Polygone selbst konstruieren:

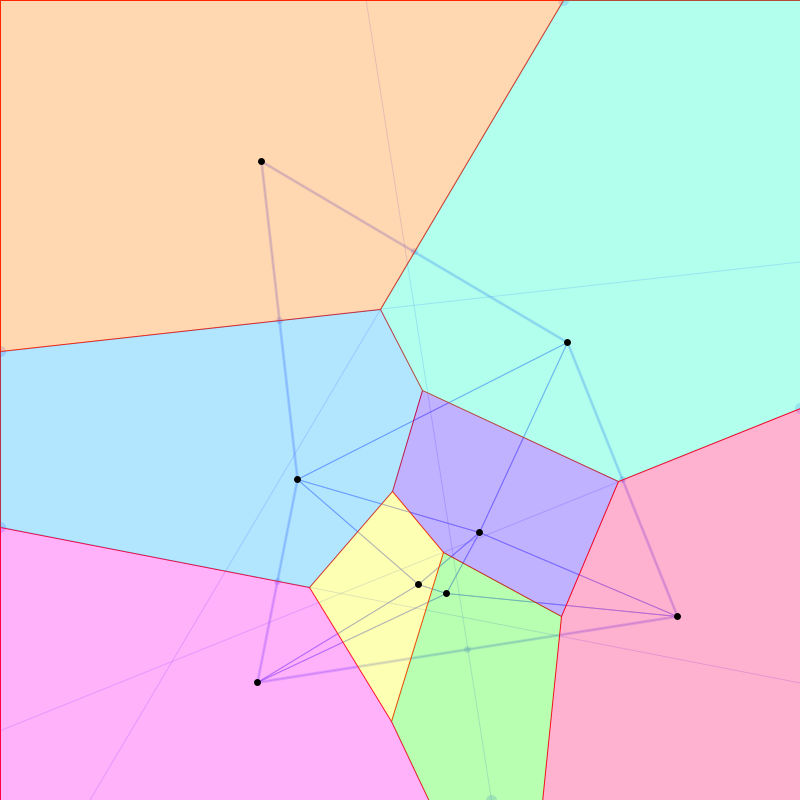Voronoi-Polygone

Zwei Sonderfälle sind beim aktuellen Stand des Algorithmus noch nicht berücksichtigt: Falls die Außenkante des Graphen aus der Delauney Triangulation zu konkav wird, schlägt der vorgestellte Algorithmus fehl - das passiert immer dann, wenn sich zwei oder mehr der aus den Mittelsenkrechten gewonnenen zusätzlichen Polygonkanten schneiden. Ein weiterer bisher nicht behandelter Sonderfall tritt ein, wenn die Punkte den gesamten Eingangsraum nicht vollständig überdecken. Dafür müsste das Auswahlkriterium der Hälften der Mittelsenkrechten angepasst werden - es darf nicht mehr allein auf der Entfernung des Mittelpunkts von den Grenzen des Eingangsraumes abhängen.

Aktualisierung vom 15. März 2022

Kommentar hinzufügen (via ) Kommentare ansehen (via )

Kommentar hinzufügen (via ) Kommentare ansehen (via )