Nachdem ich das Buch und die Videos von Steven Strogatz durch hatte, habe ich ein Experiment nachvollziehen wollen, zu dem die Idee von einem seiner Studenten gekommen war:
Ich habe zunächst das traditionelle Lorenz-System mit
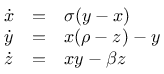benutzt. Dieses System löste ich numerisch mit je zwei unterschiedlichen Startbedingungen für eine gewisse Zeit bevor ich ein der beiden Systeme mit einer der Zustandsvariablen des anderen Systems beaufschlagte. Ich benutzte dazu den Parametersatz
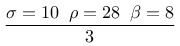Am Beispiel der Übertragung der Zustandsvariable x sieht das wie folgt aus:
Driver:
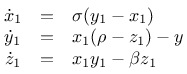
Driven:
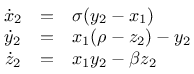
Das Ergebnis sieht man hier: in der ersten Zeile sind beide Trajektorien zum Zeitpunkt unmittelbar bevor die Kopplung erfolgt dargestellt. Man erkennt deutlich, dass die Zustände und damit die aktuelle Position im Zustandsraum beider Systeme stark voneinander abweicht. In der zweiten Zeile ist das Verhalten beider Systeme um diesen Zeitraum herum dargestellt. Man erkennt noch Unterschiede in Lage und Form der Trajektorie - schaut man sich jedoch die Position am Ende des dargestellten Ausschnitts an, kann man bereits erahnen, dass die Unterschiede immer kleiner werden. In der letzten Zeile schließlich erkennt man keine Unterschiede mehr zwischen beiden Trajektorien - Das zweite System wurde mit dem ersten nur durch die Übertragung einer Statusvariablen synchronisiert!
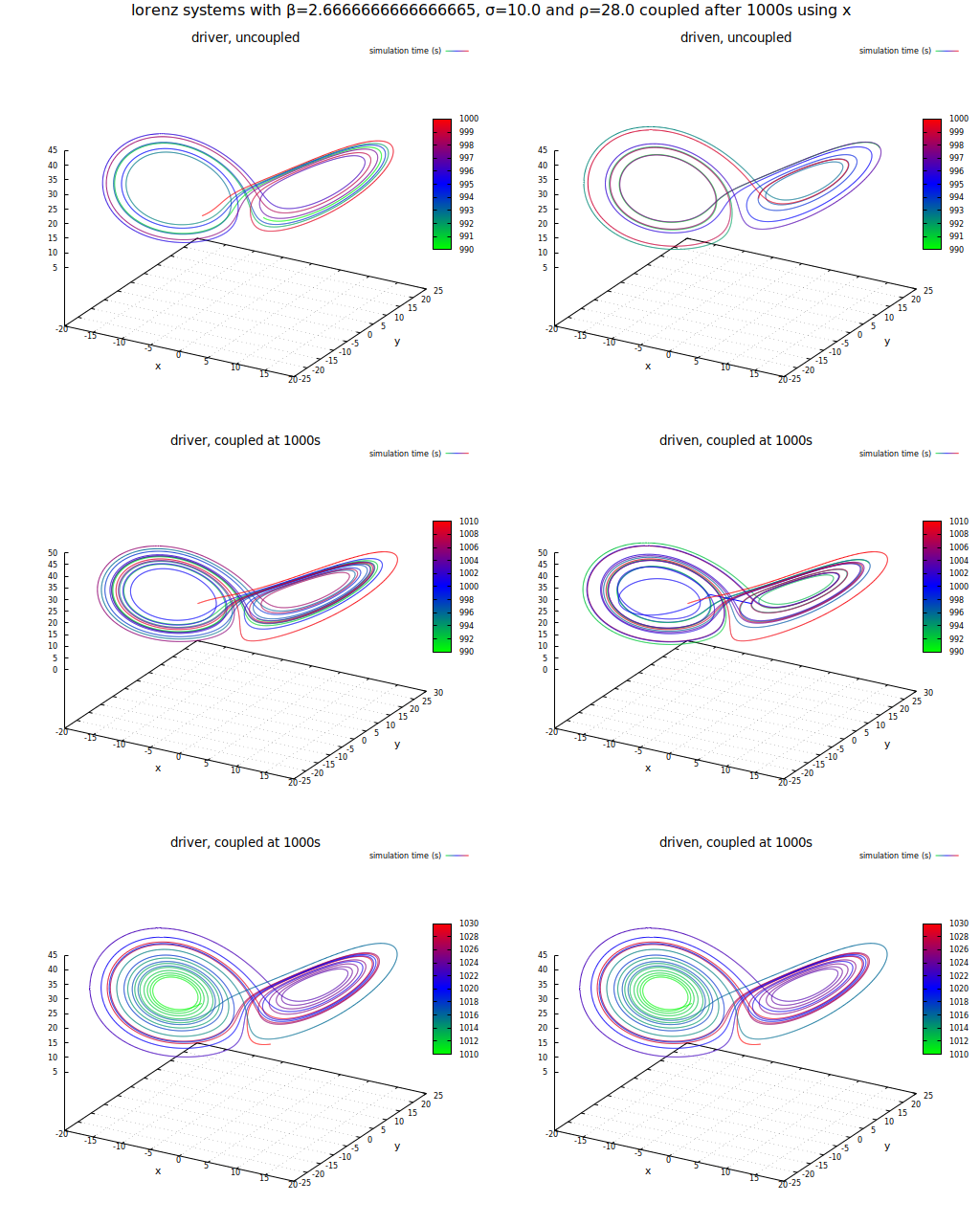Untersuchung des Verhaltens zweier Lorenz-Systeme bei Übertragung einer Statusvariablen (x)
Bei Übertragung der Statusvariablen y erkennt man exakt dasselbe Verhalten:
Driver:
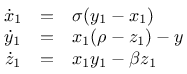
Driven:
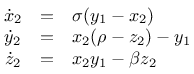
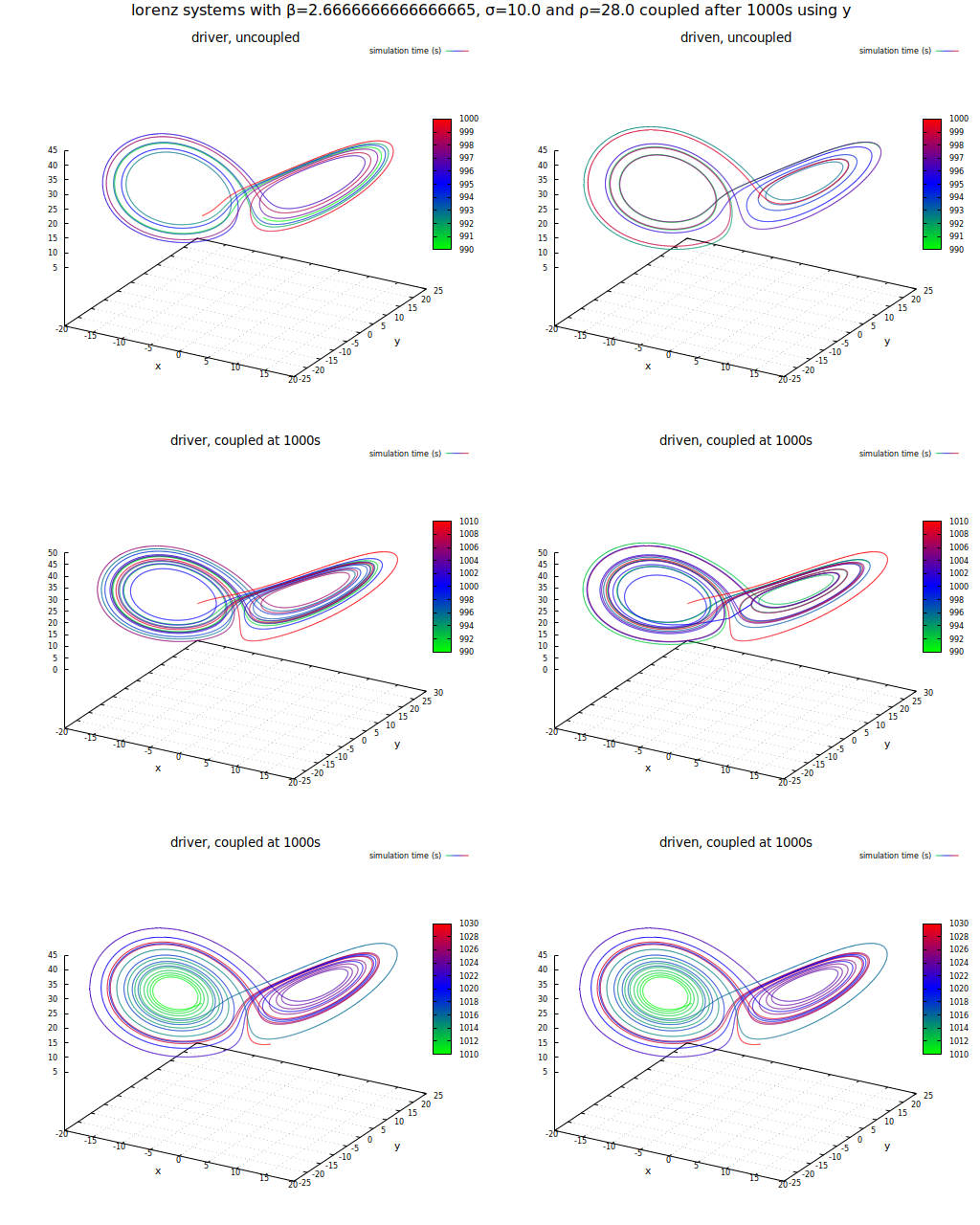Untersuchung des Verhaltens zweier Lorenz-Systeme bei Übertragung einer Statusvariablen (y)
Wie Strogatz et. al. bereits in ihren ursprünglichen Veröffentlichungen feststellten, gelingt die Synchronisation nicht mittels der Übertragung der Statusvariablen z: Man erreicht zwar eine qualitative Annäherung der Trajektorien, allerdings weichen sie qualitativ (man beachte die Skalenbeschriftungen!) stark voneinander ab.
Driver:
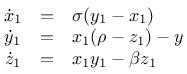
Driven:
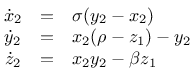
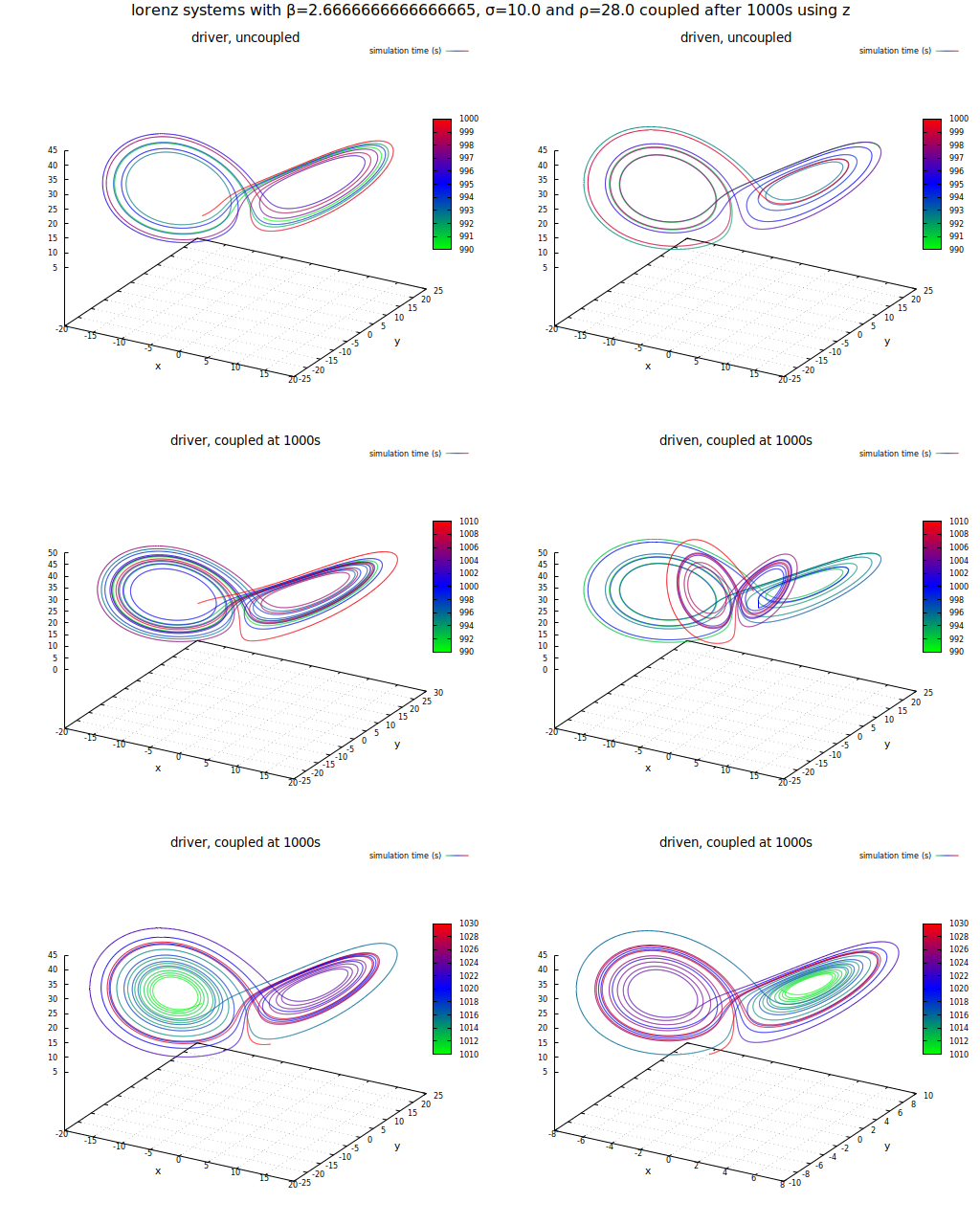Untersuchung des Verhaltens zweier Lorenz-Systeme bei Übertragung einer Statusvariablen (z)
Ich habe die Untersuchung für verschiedene Parameter wiederholt:
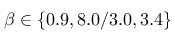
Die Ergebnisse sind im folgenden über ihre Thumbnails zu erreichen. Interessant war das Ergebnis beim Wert 0.9 und Synchronisierung über z: hier zeigte sich, dass die Synchronisation über z bei entsprechender Wahl der Parameter des Systems ebenfalls möglich ist:
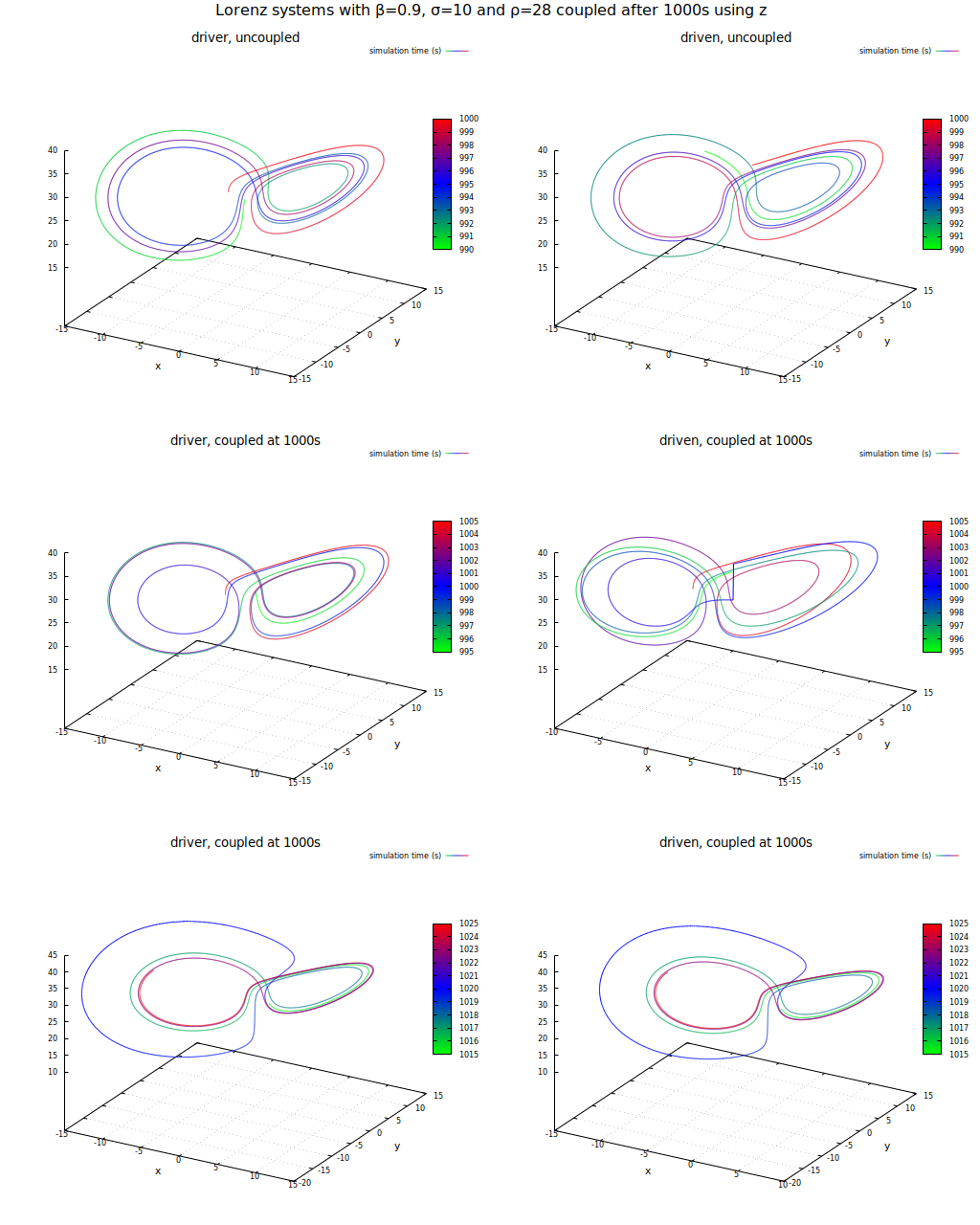Untersuchung des Verhaltens zweier Lorenz-Systeme bei Übertragung einer Statusvariablen (z) und Parametrierung mit β=0.9
Links
Synchronization in the Lorenz system
SYNCHRONIZATION OF GENERALIZED LORENZ SYSTEM USING ADAPTIVE CONTROLLER
Chaos Synchronization in Lorenz System
Chaos synchronization of the master-slave generalized Lorenz systems via linear state error feedback control
Synchronization in the Lorenz system: Stability and robustness
Synchronization of Chen’s Attractor and Lorenz Chaotic Systems by Nonlinear Coupling Function
Master-slave synchronization and the Lorenz equations
Chaos Synchronization in Lorenz System
Screenshots
Artikel, die hierher verlinken
"Funktionale" Programmierung in dWb+
31.10.2022
Nach meinem letzten Artikel zum Thema dWb+ ist bereits einige Zeit vergangen. Ich habe lange überlegt, wie ich eine Anwendung schreiben könnte, die mir gestattet, mit einem System herumzuspielen, das ich aus dem Buch von Prof.Strogatz kannte.
Synchronisierung von Lorenz-Systemen II
09.10.2020
Ich habe in einem vorhergehenden Artikel ein Paper zur Synchronisierung chaotischer Systeme nachvollzogen. Dort hatte ich gezeigt, dass - anders als im ursprünglichen Paper - eine Synchronisierung zweier gleich parametrierter Lorenz-Systeme bei geeigneter Parameterwahl auch über die Zustandsvariable z möglich ist.
Kommentar hinzufügen (via 
Kommentare ansehen (via 
Vor 5 Jahren hier im Blog
-
Fährnisse des Buildprozesses unter Windows
17.07.2019
Nachdem ich begonnen hatte, mich mit der Beschleunigung der Berechnung des Mandelbrot-Fraktals unter Zuhilfenahme der Shadereinheiten in Graphikkarten zu beschäftigen und erste Erfolge feiern konnte, wollte ich das mal auf einer richtigen Graphikkarte ausprobieren...
Weiterlesen...
Tags
Android Basteln C und C++ Chaos Datenbanken Docker dWb+ ESP Wifi Garten Geo Git(lab|hub) Go GUI Gui Hardware Java Jupyter Komponenten Links Linux Markdown Markup Music Numerik PKI-X.509-CA Python QBrowser Rants Raspi Revisited Security Software-Test sQLshell TeleGrafana Verschiedenes Video Virtualisierung Windows Upcoming...
Neueste Artikel
- Datenvalidierung UTF8 mit BiDi-Steuerzeichen (TrojanSource 2.0)
Ich bin heute nochmal inspiriert worden, weiter über die Trojan Source Vulnerability nachzudenken. Meiner Meinung nach bestehen hier noch Probleme - speziell bei Nutzereingaben oder Daten, die über externe Schnittstellen ampfangen werden.
Weiterlesen... - OpenStreetMap Navi als Docker-Container
Ich habe die auf OpenStreetMap basierende OpenSource Navigationslösung Graphhopper in einen Docker-Container gepackt und als neuestes Mitglied in meinem Docker-Zoo willkommen geheißen.
Weiterlesen... - SQL-Aggregatfunktionen in SQLite als BeanShell-Scripts
Ich habe neulich über eine Möglichkeit berichtet, SQLite mittels der sQLshell und Beanshell-Skripten um SQL-Funktionen zu erweitern. In diesem Artikel versprach ich auch, über eine solche Möglichkeit für Aggregatfunktionen zu berichten.
Weiterlesen...
Manche nennen es Blog, manche Web-Seite - ich schreibe hier hin und wieder über meine Erlebnisse, Rückschläge und Erleuchtungen bei meinen Hobbies.
Wer daran teilhaben und eventuell sogar davon profitieren möchte, muß damit leben, daß ich hin und wieder kleine Ausflüge in Bereiche mache, die nichts mit IT, Administration oder Softwareentwicklung zu tun haben.
Ich wünsche allen Lesern viel Spaß und hin und wieder einen kleinen AHA!-Effekt...
PS: Meine öffentlichen GitHub-Repositories findet man hier - meine öffentlichen GitLab-Repositories finden sich dagegen hier.
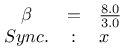
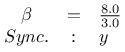
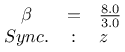
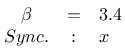
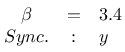
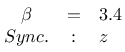
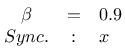
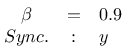
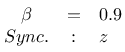