Ich bin durch Stöbern in meiner sozialen Blase auf ein altes Verfahren aufmerksam geworden, das ich dennoch bisher nicht kannte (sollte mein alter Bildverarbeitungs-Professor sich jetzt zornroten Kopfes fragen, wieso er damals dann überhaupt vor uns gestanden hat, bitte ich inständig um Vergebung für meine Unaufmerksamkeit!)

Das Verfahren ersetzt die affine Transformation des Drehes einer Bitmap-Graphik (der beliebiger zweidimensionaler Koordinaten) durch drei Scherungs-Operationen. Dabei wird die Rotation um einen bestimmten Winkel durch eine Scherung in x-Richtung, eine in y-Richtung und am Ende noch eine die Wiederholung der ersten ersetzt.

Warum das so ist? Nun, die traditionelle Rotation um einen Winkel ist definiert durch die Rotationsmatrix:

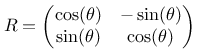
Die drei Scherungsmatrizen lauten:

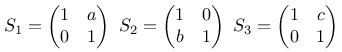
Multipliziert man diese drei Matrizen aus, erhält man die resultierende Matrix für die Transformation zweidimensionaler Koordinaten wie folgt:

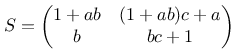
Durch Gleichsetzung

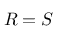
und damit

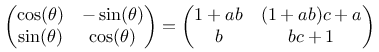
erkennt man unmittelbar, dass

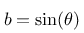
Durch Einsetzen ergibt sich

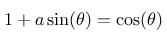
bzw:

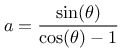
Mit

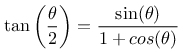
ergibt sich schließlich

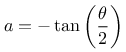
Und aus

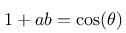
und

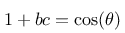
kann man

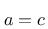
ableiten und erhält damit für die drei Parameter der Scherung:

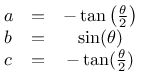
Damit wird auch ersichtlich, warum die dritte Scherung eine simple Wiederholung der ersten darstellt.

Ich habe hier drei Beispiele mit der guten alten Lena zum Vergleich abgebildet: Das erste Bild ist aus einer traditionellen Rotation kombiniert mit einer bikubischen Filterung entstanden:

Lena gedreht mittels traditioneller Rotationsmatrix

Das zweite Bild zeigt das Ergebnis mit der Variante dreier aufeinanderfolgender Scherungen:

Lena gedreht mittels dreier Scherungen ohne Filter

Und das letzte Bild schließlich demonstriert das Ergebnis mit einem etwas hemdsärmeligen Ansatz zur Filterung zur Vermeidung starker Treppenbildung (besonders ersichtlich im zweiten Bild ohne Filter am Hut):

Lena gedreht mittels dreier Scherungen mit Maßnahmen zur Reduktion von Treppenartefakten

Man erkennt auch sehr gut, dass durch die dreimalige Anwendung einer Operation mehr Bildinhalte verloren gehen als bei der Rotation - Man muss daher bei der Entscheidung für oder gegen die Variante mit denm Scherungen auch abwägen, wie wichtig die Informationen an den Rändern und in den Ecken des Originals sind!

Der Algorithmus, so wie ich ihn implementiert habe benötigt immer noch während der Ausführung Gleitkommaarithmetik. Die Parameter für die Scherung lassen sich beim Start der Anwendung in Lookup-Tabellen vorberechnen und von dort aus benutzen. Es sollte möglich sein, die Scherung ebenfalls ohne Gleitkommaarithmetik durchführen zu können - dazu könnte man etwa für die Berechnung der einzelnen Offsets der jeweiligen Zeilen und Spalten den guten alten Bresenham-Linienalgorithmus zur Anwendung bringen.

Kommentar hinzufügen (via ) Kommentare ansehen (via )

Kommentar hinzufügen (via ) Kommentare ansehen (via )